Vanishing Point Definition In Art

Attribute of perspective drawing

A vanishing betoken tin can be seen at the far end of this railroad.

A vanishing betoken is a point on the paradigm plane of a perspective drawing where the two-dimensional perspective projections of mutually parallel lines in three-dimensional space announced to converge. When the set of parallel lines is perpendicular to a picture plane, the construction is known equally one-point perspective, and their vanishing point corresponds to the oculus, or "eye point", from which the image should exist viewed for right perspective geometry.^[1] Traditional linear drawings use objects with i to three sets of parallels, defining 1 to iii vanishing points.

Italian humanist polymath and architect Leon Battista Alberti first introduced the concept in his treatise on perspective in art, De pictura, written in 1435.^[2]

Vector notation [edit]

A 2D construction of perspective viewing, showing the formation of a vanishing signal

The vanishing point may besides be referred to every bit the "direction point", as lines having the same directional vector, say D, will have the same vanishing signal. Mathematically, let $q \equiv (x, y, f)$ be a point lying on the image airplane, where $f$ is the focal length (of the photographic camera associated with the prototype), and let $5 q \equiv (x / h, y / h, f / h)$ exist the unit vector associated with $q$ , where $h = \sqrt ten 2 + y 2 + f 2$ . If nosotros consider a straight line in space $S$ with the unit vector $n southward \equiv (northward x, n y, n z)$ and its vanishing signal $five southward$ , the unit of measurement vector associated with $5 s$ is equal to $north due south$ , assuming both point towards the paradigm plane.^[three]

When the image plane is parallel to two world-coordinate axes, lines parallel to the centrality that is cut by this image plane will take images that encounter at a single vanishing indicate. Lines parallel to the other two axes volition not course vanishing points as they are parallel to the image plane. This is i-point perspective. Similarly, when the image plane intersects two world-coordinate axes, lines parallel to those planes volition run across form two vanishing points in the picture plane. This is called ii-point perspective. In three-point perspective the paradigm aeroplane intersects the $x$ , $y$ , and $z$ axes and therefore lines parallel to these axes intersect, resulting in three different vanishing points.

Theorem [edit]

The vanishing point theorem is the principal theorem in the science of perspective. It says that the image in a picture plane $π$ of a line $50$ in space, not parallel to the moving-picture show, is adamant past its intersection with $π$ and its vanishing point. Some authors accept used the phrase, "the paradigm of a line includes its vanishing point". Guidobaldo del Monte gave several verifications, and Humphry Ditton called the result the "main and Corking Proposition".^[4] Brook Taylor wrote the showtime book in English on perspective in 1714, which introduced the term "vanishing bespeak" and was the first to fully explain the geometry of multipoint perspective, and historian Kirsti Andersen compiled these observations.^[one] ^{: 244–six} She notes, in terms of projective geometry, the vanishing point is the paradigm of the bespeak at infinity associated with $L$ , as the sightline from $O$ through the vanishing indicate is parallel to $L$ .

Vanishing line [edit]

Every bit a vanishing indicate originates in a line, so a vanishing line originates in a plane $α$ that is not parallel to the picture $π$ . Given the eye signal $O$ , and $β$ the airplane parallel to $α$ and lying on $O$ , so the vanishing line of $α$ is $β \cap π$ . For example, when $α$ is the ground plane and $β$ is the horizon aeroplane, then the vanishing line of $α$ is the horizon line $β \cap π$ . Anderson notes, "Simply one item vanishing line occurs, often referred to every bit the "horizon".^[i] ^{: 249, 503–six}

To put it merely, the vanishing line of some plane, say $α$ , is obtained past the intersection of the image plane with another plane, say $β$ , parallel to the plane of involvement ( $α$ ), passing through the camera heart. For different sets of lines parallel to this plane $α$ , their respective vanishing points will prevarication on this vanishing line. The horizon line is a theoretical line that represents the eye level of the observer. If the object is below the horizon line, its vanishing lines angle up to the horizon line. If the object is above, they gradient down. All vanishing lines end at the horizon line.

Properties [edit]

1. Projections of two sets of parallel lines lying in some aeroplane $π A$ appear to converge, i.e. the vanishing bespeak associated with that pair, on a horizon line, or vanishing line $H$ formed past the intersection of the image plane with the plane parallel to $π A$ and passing through the pinhole. Proof: Consider the ground plane $π$ , as $y = c$ which is, for the sake of simplicity, orthogonal to the epitome plane. Also, consider a line $Fifty$ that lies in the airplane $π$ , which is divers by the equation $ax + bz = d$ . Using perspective pinhole projections, a point on $L$ projected on the paradigm plane volition have coordinates defined as,

x' = f \cdot x / z = f \cdot d - bz / az

y' = f \cdot y / z = f \cdot c / z

This is the parametric representation of the epitome $L'$ of the line $Fifty$ with $z$ as the parameter. When $z \to -\infty$ it stops at the indicate $(x', y') = (- fb / a,0)$ on the $x'$ centrality of the image plane. This is the vanishing indicate corresponding to all parallel lines with slope $- b / a$ in the plane $π$ . All vanishing points associated with dissimilar lines with dissimilar slopes belonging to plane $π$ will prevarication on the $x'$ centrality, which in this case is the horizon line.

ii. Let $A$ , $B$ , and $C$ exist three mutually orthogonal straight lines in space and $5 A \equiv (x A, y A, f)$ , $v B \equiv (x B, y B, f)$ , $v C \equiv (x C, y C, f)$ be the three corresponding vanishing points respectively. If nosotros know the coordinates of 1 of these points, say $v A$ , and the direction of a straight line on the image airplane, which passes through a second point, say $5 B$ , we tin can compute the coordinates of both $v B$ and $five C$ ^[iii]

three. Permit $A$ , $B$ , and $C$ be iii mutually orthogonal straight lines in infinite and $v A \equiv (10 A, y A, f)$ , $v B \equiv (x B, y B, f)$ , $five C \equiv (x C, y C, f)$ be the three corresponding vanishing points respectively. The orthocenter of the triangle with vertices in the 3 vanishing points is the intersection of the optical axis and the image plane.^[3]

Curvilinear and opposite perspective [edit]

A curvilinear perspective is a drawing with either 4 or 5 vanishing points. In 5-bespeak perspective the vanishing points are mapped into a circumvolve with iv vanishing points at the fundamental headings N, W, S, Due east and one at the circumvolve's origin.

A reverse perspective is a drawing with vanishing points that are placed outside the painting with the illusion that they are "in front of" the painting.

Single bespeak perspective projection.
Unmarried betoken perspective in photography
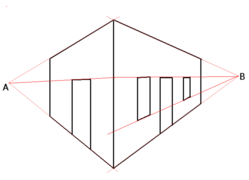
Double point perspective projection.

Detection [edit]

Several methods for vanishing point detection make use of the line segments detected in images. Other techniques involve because the intensity gradients of the image pixels directly.

There are significantly big numbers of vanishing points present in an paradigm. Therefore, the aim is to detect the vanishing points that represent to the principal directions of a scene. This is more often than not achieved in two steps. The first step, chosen the accumulation footstep, as the proper noun suggests, clusters the line segments with the assumption that a cluster will accept a common vanishing signal. The next pace finds the principal clusters present in the scene and therefore information technology is called the search footstep.

In the accumulation stride, the paradigm is mapped onto a divisional space called the accumulator space. The accumulator space is partitioned into units called cells. Barnard ^[v] causeless this infinite to be a Gaussian sphere centered on the optical centre of the camera as an accumulator space. A line segment on the image corresponds to a great circle on this sphere, and the vanishing betoken in the image is mapped to a signal. The Gaussian sphere has accumulator cells that increment when a great circle passes through them, i.e. in the image a line segment intersects the vanishing betoken. Several modifications have been made since, only i of the most efficient techniques was using the Hough Transform, mapping the parameters of the line segment to the divisional space. Cascaded Hough Transforms have been applied for multiple vanishing points.

The process of mapping from the image to the bounded spaces causes the loss of the actual distances between line segments and points.

In the search step, the accumulator cell with the maximum number of line segments passing through it is found. This is followed by removal of those line segments, and the search footstep is repeated until this count goes below a certain threshold. Every bit more computing power is now available, points corresponding to two or three mutually orthogonal directions tin be establish.

Applications [edit]

Utilize of cross-ratios in projective geometry to measure out real-earth dimensions of features depicted in a perspective project. A, B, C, D and 5 are points on the image, their separation given in pixels; A', B', C' and D' are in the real world, their separation in metres.

In (i), the width of the side street, W is computed from the known widths of the adjacent shops.
In (2), the width of only 1 shop is needed because a vanishing signal, V is visible.

Camera calibration: The vanishing points of an image contain important information for camera scale. Diverse calibration techniques have been introduced using the backdrop of vanishing points to observe intrinsic and extrinsic calibration parameters.^[6]
3D reconstruction: A human being-made environment has ii master characteristics – several lines in the scene are parallel, and a number of edges present are orthogonal. Vanishing points assistance in comprehending the environment. Using sets of parallel lines in the aeroplane, the orientation of the plane tin be calculated using vanishing points. Torre ^[vii] and Coelho ^[8] performed extensive investigation in the apply of vanishing points to implement a full organisation. With the assumption that the environs consists of objects with simply parallel or perpendicular sides, as well called Lego-land, using vanishing points constructed in a single image of the scene they recovered the 3D geometry of the scene. Like ideas are also used in the field of robotics, mainly in navigation and autonomous vehicles, and in areas concerned with object detection.

See likewise [edit]

Graphical project

References [edit]

^ ^a ^b ^c Kirsti Andersen (2007) Geometry of an Art, p. 30, Springer, ISBN 0-387-25961-9
^ Wright, D. R. Edward (1984). "Alberti's De Pictura: Its Literary Structure and Purpose". Periodical of the Warburg and Courtauld Institutes. 47: 52–71. doi:10.2307/751438. JSTOR 751438. S2CID 195046955.
^ ^a ^b ^c B. Caprile, Five. Torre [1] "Using Vanishing Points for Camera Scale", International Journal of Reckoner Vision, Book 4, Event 2, pp. 127-139, March 1990
^ H. Ditton (1712) Treatise on Perspective, p 45
^ Due south.T. Barnard 'Interpreting Perspective Images", Artificial Intelligence 21, 1983, pp. 435 - 462
^ D. Liebowitz and A. Zisserman "Metric Rectification for perspective images of planes" ,IEEE Conf. Figurer Vision and Pattern Recognition, June 1998, Santa Barbara, CA, pp. 482 -488
^ R.T. Collins, and R. Weiss "Vanishing Signal Calculation every bit a Statistical Inference on the Unit Sphere" Proceedings of ICCV3, December, 1990
^ C. Coelho, Thousand. Straforani, M. Campani " Using Geometrical Rules and a priori Knowledge for the Understanding of Indoor Scenes" Proceedings BMVC90, p.229-234 Oxford, September 1990.

External links [edit]

Vanishing bespeak detection by three different proposed algorithms
Vanishing point detection for images and videos using open CV
A tutorial covering many examples of linear perspective
Trigonometric Adding of Vanishing Points Cursory explanation of the rationale with an easy instance